In the past decade, exploration for new types of topological insulators is substantively followed up in different subfields of physics, making a paradigm shift for topological states, from electronics to photonics, phononics as well as mechanics.

In photonics, the field of topological insulators is rapidly developing in the past few years, where one of most representative example should be the Floquet topological insulator, proposed in periodically driven systems.

Most recently, researchers from several universities and research institutes work together to have represented an important step in the implementation of a diverse family of topological structures and networks for sound with new properties and functionalities. They provide a fertile ground for novel wave manipulations, such as the unidirectional sound transports and robust sound transports against perturbations, and push forward the fundamental explorations of topological acoustics. Their research results have been published in Nature Communications.

Researchers have theoretically proposed and experimentally demonstrated the anomalous Floquet topological insulator for sound: a strongly coupled metamaterial ring lattice that supports one-way propagation of pseudo-spin-dependent edge states under T-symmetry. As well, researchers also demonstrate the formation of pseudo-spin-dependent interface states due to lattice dislocations and investigate the properties of pass band and band gap states.

The model of anomalous Floquet topological insulator is a 2D coupled metamaterial ring lattice, presented in Fig. 1. It can support topological edge states at sufficiently large coupling strength between neighbouring lattice rings.

A pseudo-spin for acoustic waves is defined based on wave circulation direction in the lattice rings viz. pseudo-spin-up↔clockwise and pseudo-spin-down↔anti-clockwise. By purposely designing the lattice configuration, researchers have successfully constructed the acoustic anomalous Floquet topological insulator. It can support the pseudo-spin-dependent edge states, scattering immune to boundary abrupt variations or lattice dislocations.

The edge states with different pseudo-spins can propagate in opposite directions under T-symmetry at the same boundary, shown in Fig. 2. Researchers emphasize that the edge states with different pseudo-spins are regarded as decoupled due to nearly unitary coupling between neighbouring rings, closing the time-reversed channels for backscatterings. In this case, the rings no longer act as resonators and the edge state is essentially a conventional waveguide mode.

For one specific pseudo-spin, there exists a pair of edge states propagating along the upper and lower boundaries, respectively, with opposite group velocities. The observations reveal that when the coupling strength between adjacent lattice rings surpasses a threshold, acoustic waves carrying a pseudo-spin in one lattice ring may tunnel into the neighbouring coupling ring with the pseudo-spin flipped. And then, they go to another lattice ring with the pseudo-spin restored or conserved, rendering an interesting zigzag route.

Of interest will be the extension of this research into non-reciprocal acoustics regime by integrating time-varying (for example, rotating the metamaterial rings), shedding lights on the development of chiral acoustic metamaterials and Chern acoustic topological insulators with various intriguing non-reciprocal properties, such as one-way sound isolation.

Fig. 1 Photograph of the fabricated samples (Image by JIA Han et al.)

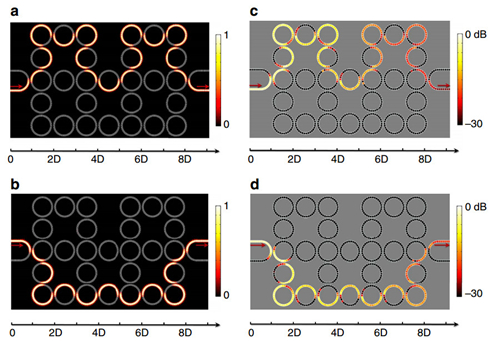
Fig. 2 The simulated (a, b) and measured (c, d) pressure amplitude distributions of one-way edge states (Image by JIA Han et al.)

Reference:

PENG Yugui Peng, QIN Chengzhi, ZHAO Degang, SHEN Yaxi, XU Xiangyuan, BAO Ming, JIA Han, and ZHU Xuefeng. Experimental Demonstration of Anomalous Floquet Topological Insulator for Sound. Nature Communications 7: 13368. (November 11 2016) DOI:10.1038/ncomms13368

Contact:

JIA Han

Key Laboratory of Noise and Vibration Research, Institute of Acoustics, Chinese Academy of Sciences, 100190 Beijing, China

E-mail: hjia@mail.ioa.ac.cn