Adaptive filters have wide applications in general signal processing applications, such as acoustic echo/feedback cancellation, active noise control, source localization and so on. Recursive least square (RLS) is a ubiquitous adaptive filtering algorithm used in general adaptive signal processing applications.
Among those adaptive filters, the RLS enjoys fast convergence with acceptable computational and storage complexity. However, the RLS is very sensitive to the interferences which rarely appear but with strong transient energy, i.e. outlier.
Traditional robust RLS has difficulties to cope with correlated ambient noise. Based on robust statistics, traditional robust RLS algorithms have been reported to recursively minimize some modified non-convex cost function. Nevertheless, these models cannot handle the cases with correlated ambient nominal noise.
To provide robustness in such cases, several researchers from the Key Laboratory of Noise and Vibration Research of the Chinese Academy of Sciences have proposed a robust RLS via outlier pursuit (RRLSvOP) framework. The framework is designed with outlier's sparsity control via possibly non-convex penalties, such as the minimax concave penalty (MCP). It has been proved that it benefits from recent progress of Compressed Sensing (CS) and its connections to robust statistics.
The key ingredients of the framework depends on a new data generation model under possible outlier corruptions as,
![]()
where y(n) and X(n) are known outputs and inputs of a dynamic linear system, wo(n) is unknown parameter vector to be estimated, o(n) and v(n) are sparse and dense noise vectors, respectively.
In the model, the explicit modeling of outlier components is the basis of the connections of robust statistics and compressed sensing. With this new model, the researchers propose to solve a penalized optimization problem,
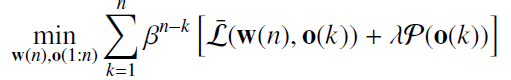
where
![]()
and the penalty ![]() is some sparsity prompting functions, such as L1, MCP, etc.
is some sparsity prompting functions, such as L1, MCP, etc.
Because of the non-convexity of the proposed model, more advanced numerical procedures with convergence guarantees, such as multi-stage convex relaxation (MSCR), coordinate descent (CD), proximal gradient (PG) and PG with homotopy (PGH), are adapted in the online update stage, while the initialization stage is solved via MSCR strategy.
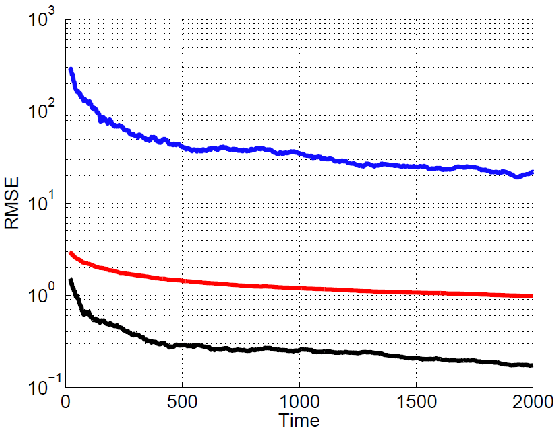
Fig. 1. RMSE convergence curves for RRLSvOP. The problems with L1 and MCP penalties are solved via MLLA-CVX solver at the initialization stage, then at the online update stage PGH is used. In the figure, each solid line corresponds to the result for, from top to down, RLS, RRLSvOP-L1 and RRLSvOP-MCP, respectively (Image by XIAO).
Simulations demonstrate improved robustness of the method using non-convex penalty (e.g., MCP) in comparison with the one using L1 penalty. Fig. 1 shows the benefits of non-convex penalty versus L1 penalty in both the initialization stage and online update stage. Note that both of them, convex or non-convex penalties, outperform ordinary RLS significantly when measurements contain outliers.
Results also show that under the correlated dense noise case, the proposed RRLSvOP with non-convex penalty can provide online robust estimates up to 50 percentage of outlier contaminations, whereas the convex one fails to provide such kind of robustness.
Funding for this research came from the National Natural Science Foundation of China (Grant No.11474306, No.11174317, No.11474307, No.11404367).
Reference:
XIAO Longshuai, WU Ming, YANG Jun and TIAN Jing. Robust RLS via the Nonconvex Sparsity Prompting Penalties of Outlier Components. Signal and Information Processing (ChinaSIP), 2015 IEEE China Summit and International Conference on, Chengdu, China, pp.997-1001, 12-15 July, 2015. DOI: 10.1109/ChinaSIP.2015.7230554
Contact:
XIAO Longshuai
Institute of Acoustics, Chinese Academy of Sciences, 100190 Beijing, China
Email: xls.ioa@gmail.com


