Keywords: Layered half-space; Porous layers; Rayleigh waves; Dispersion
Porous formation is one of the most common formations in geophysical and engineering geophysical exploration, and one of the most important objects for oil and gas resources exploration. Therefore, getting accurate parameters of porous media is a significant work of oil and gas resources exploration. Exploration by Rayleigh waves is one of the most effective engineering explorations, though which is founded on elastic layered half-space.
It would be difficult if Rayleigh waves exploration is applied in porous layered half-space. To solve this problem, researchers from the Institute of Acoustics of the Chinese Academy of Sciences have theoretically researched on the dispersion function and excitation mechanism of Rayleigh waves in porous layered half-space.
The dispersion function of Rayleigh waves in layered half-space with porous layers is different from that in elastic layered half-space, and it is relevant with the porous layers’ position. For the different positions of porous layers, the dispersion function of Rayleigh waves is deduced by the boundary and propagation condition. Moreover, the surface displacements of Rayleigh waves excited by both explosive point source and surface normal force source are computed.
The transfer matrix method is always used in theoretical research of acoustic propagation in layered media. It is a simple and effective means to calculate the dispersion curves. However, this method has a limitation that it may cause the significant digit losing in high frequency range. In the porous layer, the problem is even harder due to the slow longitude wave and the dissipation effect.
Furthermore, an optimized algorithm of transfer matrix is proposed to improve the significant digit lost problem in high frequency area, improving precision as well as speed of the dispersion function of Rayleigh waves in layered half-space with porous layers. Based on the characteristics of the dispersion function, the transfer matrix of layered half-space is rebuilt with porous layers, and the matrix form of multiplied triple 6×6 to a square matrix of 15×15 is simplified.
Therefore, both the accuracy and frequency range of the dispersion computation are all improved. Finally, the bisection method is introduced into complicated plane to get the complicated roots of the dispersion functions, using these roots as the initial values of Newton-Raphson method.
The figures of dispersion curves calculated by original and optimized transfer matrix are shown in Fig. 1. From these figures, it shows that the computable frequency range is only about 12 kHz for the original method (left), but it is up to 22 kHz for the optimized one (right). In addition, the original method would lose some modes because of the calculation limitation: the 4th and 5th modes are missed in the left figure of Fig. 1.
As a result, the problem of how Rayleigh waves exploration can be applied on a porous layered half-space is well solved in this optimized method.
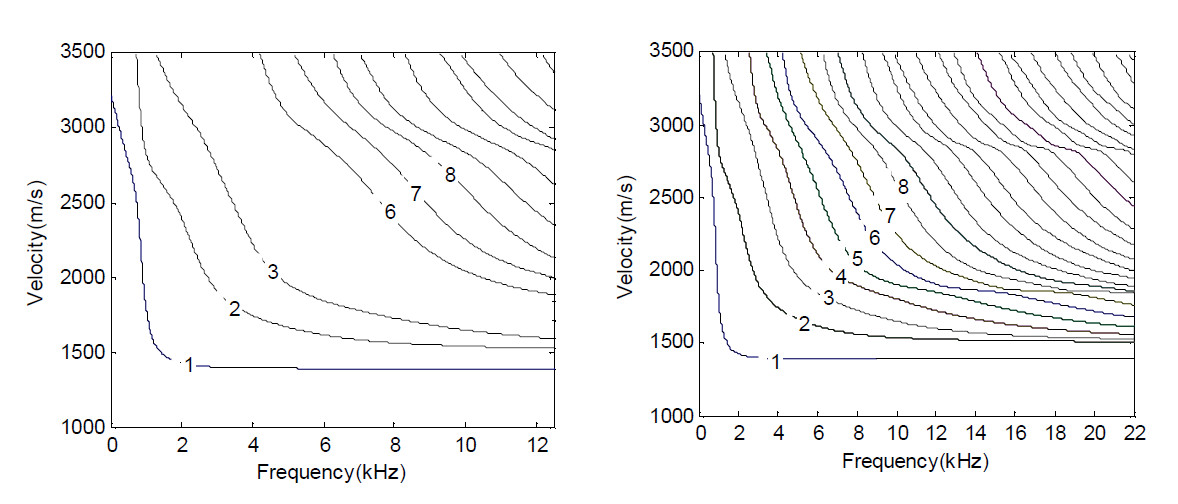
Fig.1. The comparison of the dispersion curves calculated by the original and optimized transfer matrix (Image by YAN)
References:
YAN Shouguo, XIE Fuli, ZHANG Bixing. The Algorithm of Dispersion Function of Rayleigh Waves' in Porous Layered Half-Space. Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), 2014 Symposium on, ISBN 978-1-4799-6424-6, IEEE (pp. 331-334, Oct. 30 2014-Nov. 2, 2014, Beijing, China). DOI: 10.1109/SPAWDA.2014.6998593
Contact:
YAN Shouguo
Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China
Email: yanshouguo@mail.ioa.ac.cn


