Dispersion equation is an important tool for analyzing propagation properties of acoustic waves in layered structures. And the Love wave (LW) is a kind of layered wave with particle displacement only in the shear horizontal direction. Toward LW sensors, the dispersion equation with an isotropic-considered substrate is too rough to get accurate solutions. Meanwhile, the full dispersion equation with a piezoelectric-considered substrate is too complicated to get simple and practical expressions for optimizing LW-based sensors.
The most commonly used substrate of LW-based sensors has a small piezoelectricity and a strong anisotropy. Recently, based on this analysis, Dr. LIU Jiansheng from the Institute of Acoustics, Chinese Academy of Sciences has launched a simple and accurate theoretical model for LW-based sensors. A new dispersion equation (Eq. 1) is introduced for LWs, in a layered structure with an anisotropic-considered substrate and an isotropic guiding layer. Based on the equation, an intuitive expression (Eq. 2) for mass sensitivity is also derived.
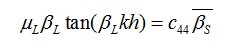 (1)
(1)
 (2)
(2)
The new equations are in simple forms similar to the simplified model with an isotropic substrate. With Love waves in an elastic SiO2 layer on an ST-90˚X quartz structure, for example, comparisons are carried out between the velocities and normalized sensitivities. It is calculated using different dispersion equations and corresponding mass sensitivities. Numerical calculations show that the new method has very precise results.
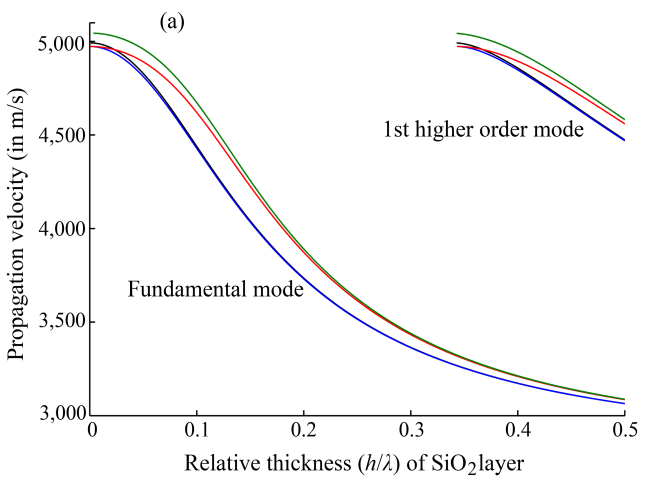

Fig. 1. Comparison between the propagation velocities of the first two Love modes in a device with an elastic SiO2 layer on a differently considered ST-90˚X quartz substrate. (a) Propagation velocity vs. relative guiding layer thickness, (b) Deviations of propagation velocity with differently simplified substrate from the exact values (Image by LIU).
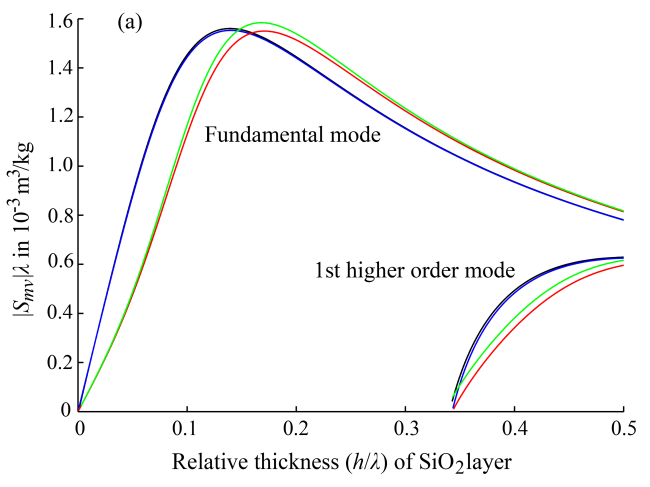
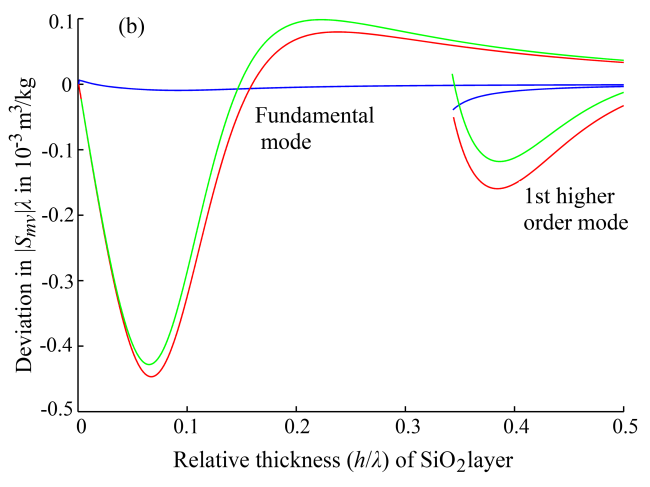
Fig. 2. Comparison between the magnitudes of normalized mass velocity sensitivity for the first two Love modes in a device with an elastic SiO2 layer on a differently considered ST-90˚X quartz substrate. (a) The magnitudes of normalized sensitivity vs. relative guiding layer thickness, (b) Deviations of the sensitivity with differently simplified substrate from the exact values (Image by LIU).
The viscoelasticity of a polymer guiding layer is described by using a model which consists of springs and dashpots. The mass velocity sensitivity and the mass propagation loss sensitivity are obtained from the real part and the imaginary part of the complex mass sensitivity, respectively. Another numerical calculation is carried out for the case of a LW sensor with a viscoelastic guiding layer. If the viscosity of the layer is not too big, the propagation loss and the mass loss sensitivity are proportional to the viscosity of the guiding layer.
References:
LIU Jiansheng. A Simple and Accurate Model for Love Wave Based Sensors: Dispersion Equation and Mass Sensitivity. AIP Advances4, 2014, 077102 (1-11).
Contact:
LIU Jiansheng
Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China


