Simple Harmonic Motion:
In order for mechanical oscillation to occur, a system must posses two quantities: elasticity and inertia. When the system is displaced from its equilibrium position, the elasticity provides a restoring force such that the system tries to return to equilibrium. The inertia property causes the system to overshoot equilibrium. This constant play between the elastic and inertia properties is what allows oscillatory motion to occur. The natural frequency of the oscillation is related to the elastic and inertia properties by:

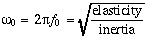
The simplest example of an oscillating system is a mass connected to a rigid foundation by way of a spring. The spring constant k provides the elastic restoring force, and the inertia of the mass m provides the overshoot. By applying Newton's second law F=ma to the mass, one can obtain the equation of motion for the system:

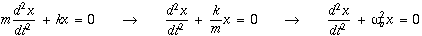
where 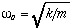 is the natural oscillating frequency. The solutions to this equation of motion takes the form

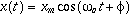
where x_m is the amplitude of the oscillation, and ?ՠis the phase constant of the oscillation. Both x_m and ?ՠare constants determined by the initial condition (intial displacement and velocity) at time t=0 when one begins observing the oscillatory motion.

Theperiodof the oscillatory motion is defined as the time required for the system to start one position, complete a cycle of motion and return to the starting position.
⇒ From the position versus time plot, can you determine the period for each of the three oscillators?

 

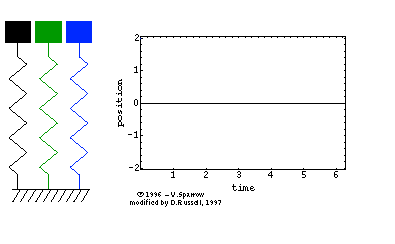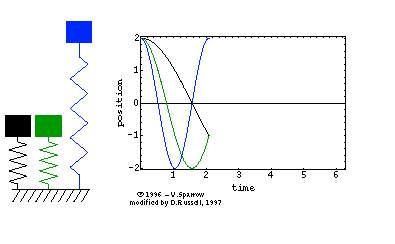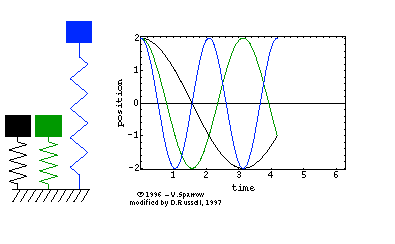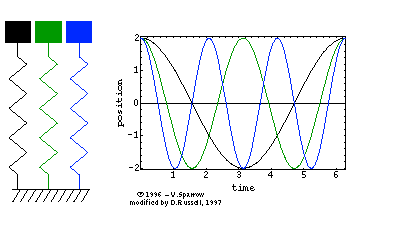
Energy Swapping:
The elastic property of the oscillating system (spring) stores potential energy

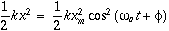
and the inertia property (mass) stores kinetic energy

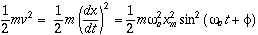
As the system oscillates, the total mechanical energy in the system trades back and forth between potential and kinetic energies. The total energy in the system, however, remains constant, and depends only on the spring contant and the maximum displacement (or mass and maximum velocity v_m=?ظ_m)

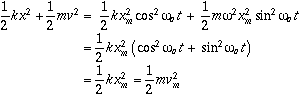
The movie at right (25 KBQuicktimemovie) shows how the total mechanical energy in a simple undamped mass-spring oscillator is traded betweenkineticandpotentialenergies while the total energy remains constant.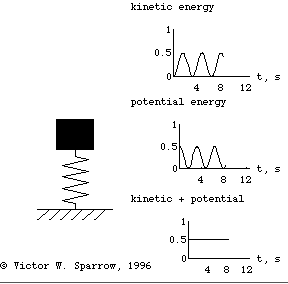