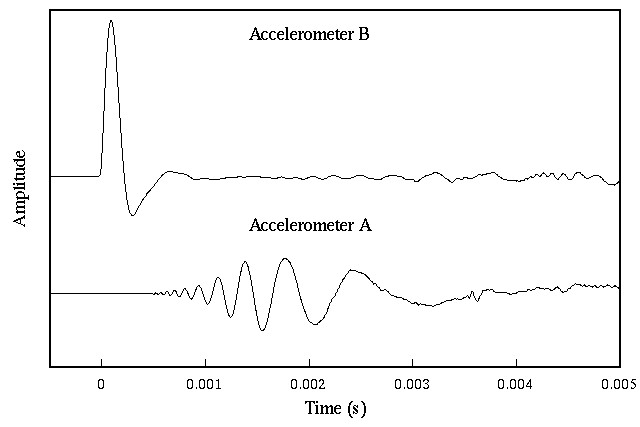
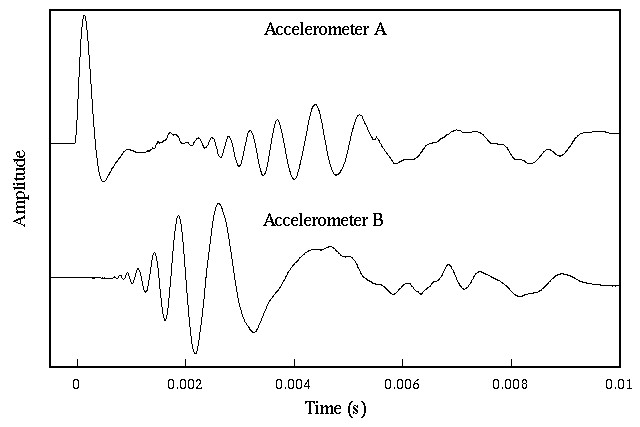
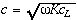A simple experiment can be performed to demonstrate the dispersive nature of flexural waves
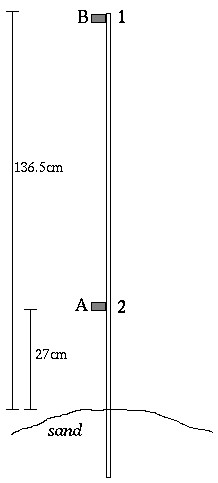
- An aluminum bar of cross-section 1/4 x1/2 inch and length 6 ft is vertically inserted in sand so that 4.48 ft (136.5 cm) is allowed to freely vibrate in a horizontal direction.
- The sand acts as a non-reflective boundary so that any flexural waves incident upon the sand will be completely absorbed.
- PCB accelerometers (1 gram) are attached at positionsAandB
- Aluminum bar is excited with an impulse, using PCB hammer with plastic tip, at points1and2
- The time signals measured by the accelerometers are displayed on an oscilloscope (one that can store a trace)
Discussion of Time Signals
The equation of motion for flexural (bending) waves in a beam is
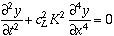
where 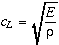 is the speed of a quasi-longitudinal wave (Eis Young's modulus and ?Ѡis the mass density). This equation of motion is a fourth-order differential equation such that the solutions are not of the formy(x,t) = f(x-ct) + g(x+ct). In addition, the flexural wave speed is dispersive is the speed of a quasi-longitudinal wave (Eis Young's modulus and ?Ѡis the mass density). This equation of motion is a fourth-order differential equation such that the solutions are not of the formy(x,t) = f(x-ct) + g(x+ct). In addition, the flexural wave speed is dispersive
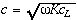
as evidenced by the fact that the wave speed is proportional to the square root of frequency. Thus, higher frequency flexural waves will travel faster than lower frequency flexural waves.
A force pulse contains many (almost infinite) frequency components
Hammer impact at Point 1
| 



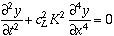
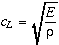 is the speed of a quasi-longitudinal wave (Eis Young's modulus and ?Ѡis the mass density). This equation of motion is a fourth-order differential equation such that the solutions are not of the formy(x,t) = f(x-ct) + g(x+ct). In addition, the flexural wave speed is dispersive
is the speed of a quasi-longitudinal wave (Eis Young's modulus and ?Ѡis the mass density). This equation of motion is a fourth-order differential equation such that the solutions are not of the formy(x,t) = f(x-ct) + g(x+ct). In addition, the flexural wave speed is dispersive