The animations on this page were inspired by figure VI/7 on page 509 of Structure-Borne Sound, Second Edition, by Heckl, Cremer and Ungar, (Springer-Verlag, 1988)

Radiation from a Cylindrical Source

The following animations illustrate the radiation of sound waves from a vibrating source in 2-D. The source is a long cylinder which is oscillating in the radial direction only (all vibrations along the length of the cylinder are ignored). In particular, the animations show the vibration of the cylinder in its various modes and the resulting particle displacements of the surrounding fluid.

Modes of a vibrating cylinder

Here is where the math equations for the modes of a vibrating cylinder go. The movie below shows the first six modes of a cylinder undergoing radial vibration. The modes are not animated at their respective frequencies.

Sound Radiation in 2-D (Hankel functions)

Here is where the math for 2-D waves (Hankel functions) which was used to generate the movies goes.

n=0 (breathing mode) => Monopole

The first mode of the cylinder corresponds to a breathing mode in which the cylinder radius expands and contracts, all parts of the cylinder moving inward or outward at the same rate. The movie at left (0.5 MB mpeg) shows the motion of the cylinder as well as the resulting motion of the particles in the fluid surrounding the cylinder. Each particle oscillates back and forth about some equilibrium radius (in order to improve the visual effect, the actual particle displacements have been amplified by a power of 2). However, the phase of their relative motions produces an outward travelling spherical wave. The wavefronts (point of constant phase) are circles, and the maximum particle displacement is the same at any point on a wavefront.

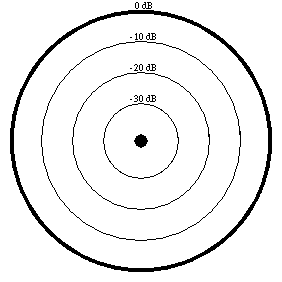This type of sound source is called a monopole. It radiates sound equally well in all directions. The figure at left shows how the sound pressure radiated by a monopole source varies with angle. The figure clearly shows that the sound pressure is the same for all angles.

n=1 (oscillating sphere) => Dipole

The second mode of the cylinder is actually a bending mode in which the entire cylinder oscillates back and forth, all parts of the cylinder moving in the same direction at the same time. The movie at left (0.486 MB mpeg) shows the motion of the cylinder as well as the resulting motion of the particles in the fluid surrounding the cylinder. Each particle oscillates back and forth about some equilibrium radius (actual particle displacements have been amplified by a power of 2).

This type of sound source is called a dipole. The sound field of a dipole is the same as for two identical but opposite phase monopoles. A dipole sound very well in two preferred directions, but does not radiate sound at all along the plane inbetween the two oppositely phased sources. The figure at left shows how the sound pressure radiated by a dipole source varies with angle.

n=2 (bell mode) => Quadrupole

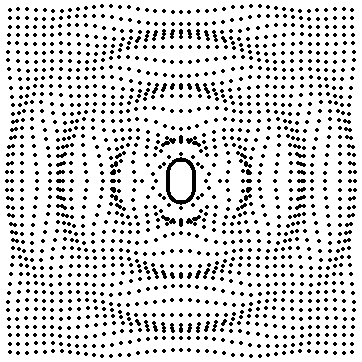The second mode of the cylinder is called the "bell mode" becuase the cylinder cross sections alternately squishes and expandes along the horizontal and vertical axes, much like the fundamental mode of a vibrating bell. The movie at left (0.475 MB mpeg) shows the motion of the cylinder as well as the resulting motion of the particles in the fluid surrounding the cylinder. Each particle oscillates back and forth about some equilibrium radius (actual particle displacements have been amplified by a power of 10). However . . .

This type of sound source is called a quadrupole. The sound field of a quadrupole is the same as for two identical but opposite phase dipoles. A dipole sound very well in four preferred directions, but does not radiate sound at all along two planes inbetween the two orientations of oppositely phased dipole sources. The figure at left shows how the sound pressure radiated by a dipole source varies with angle.

n=3

particle motions magnified 20 times

n=4 Octupole

particle motions magnified 80 times

n=6 (no farfield exists)

particle motions magnified 1000 times

(From Acoustics and Vibration Animations - Dan Russell, Kettering University)