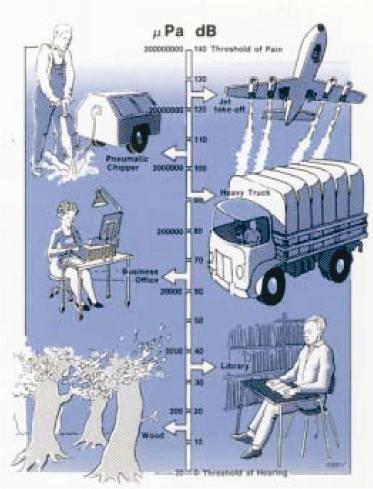
The second main quantity used to describe a sound is the size or amplitude of the pressure fluctuations. The weakest sound a healthy human ear can detect has an amplitude of 20 millionths of a Pascal (20 uPa) -- some 5000000000 times less than normal atmospheric pressure. A pressure change of 20 uPa is so small that it causes the eardrum to deflect a distance less than the diameter of a single hydrogen molecule. Amazingly, the ear can tolerate sound pressures more than a million times higher. Thus, if we measured sound in Pa, we would end up with some quite large, unmanageable numbers. To avoid this, another scale is used -- the decibel or dB scale.

The decibel is not an absolute unit of measurement. It is a ratio between a measured quantity and an agreed reference level. The dB scale is logarithmic and uses the hearing threshold of 20 uPa as the reference level. This is defined as 0 dB. When we multiply the sound pressure in Pa by 10, we add 20 dB to the dB level.So 200 uPa corresponds to 20 dB (re 20 uPa), 2000 uPa to 40 dB and so on. Thus, the dB scale compresses a range of a million into a range of only 120 dB. The sound pressure levels (SPL) in dB and Pa of various familiar sounds are shown in the figure.

One useful aspect of the decibel scale is that it gives a much better approximation to the human perception of relative loudness than the Pascal scale. This is because the ear reacts to a logarithmic change in level, which corresponds to the decibel scale where 1 dB is the same relative change everywhere on the scale. (from Bruel & Kjar)