Acoustic impedance is the intrinsic property of a structure. Different from the point impedance of fluid and the local impedance in a honeycomb structure, the acoustic impedance of an elastic structure is nonlocal and strictly global. In general, the acoustic excitation applied locally to a structure can induce vibration of the entire structure. There is a coupling effect between the acoustic medium and elastic structure, especially in water, the coupling effect is more obvious,. and correspondingly, the acoustic impedance shows stronger non-local properties.

Based on the acoustic impedance integral operator, researchers from the Institute of Acoustics of the Chinese Academy of Sciences (IACAS) proposed the concept of global acoustic impedance to describe the relationship between the acoustic excitation and the particle vibration velocity on the entire surface of an elastic structure. They also studied the method of solving the global acoustic impedance matrix and its characteristics are also studied.

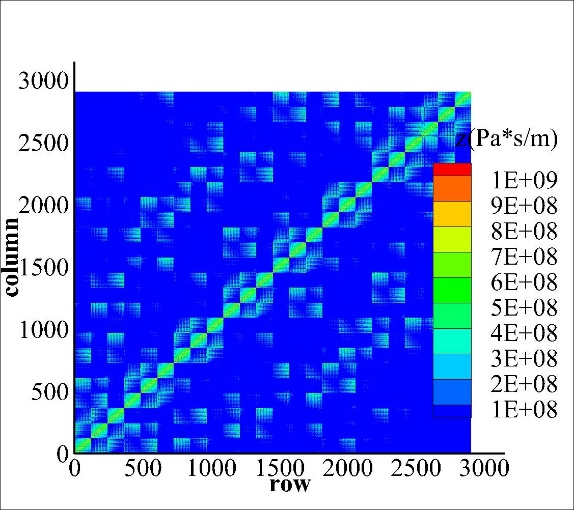
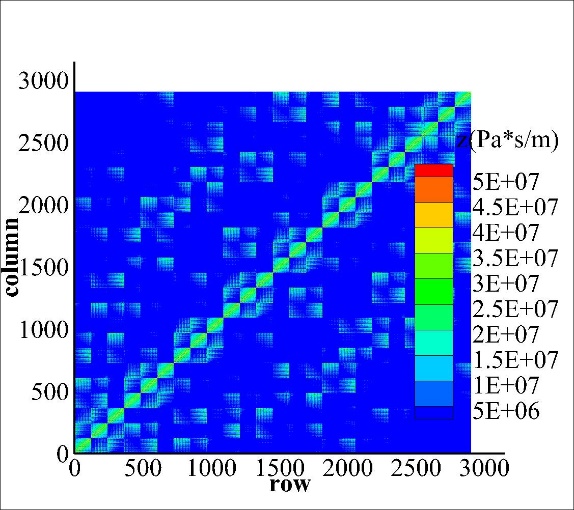
The global acoustic impedance presents the form of acoustic impedance matrix when the surface of the structure is discretized. Based on structural dynamics finite element and virtual displacement principle, researchers transferred the surface sound pressure and structural point force, and the surface vibration velocity of unit node and the vibrating velocity at the central configuration point, programming to calculate the global acoustic impedance matrix (Figure 1) of an elastic spherical shell. The spatial distribution characteristics, changing with distance (Figure 2) and frequency of the global acoustic impedance matrix were analyzed.

The global acoustic impedance can be used as a boundary condition for the calculation of acoustic scattering. The global acoustic impedance of an elastic spherical shell is relatively “rigid” in-air but “elastic” in-water. (Figure 3). The researchers also compared the TS of the underwater spherical shell corresponding to the global and local acoustic impedances, and pointed out the obvious differences between them. Global acoustic impedance provides a new data form for studying the acoustic properties of underwater structures, which is applicable not only to elastic structures but also to viscoelastic structures.

 (a)           (b)

Figure 1. Magnitude of the global acoustic impedance matrix of the elastic spherical shell. (a): at 100Hz；(b): at 2000Hz. (Image by IACAS)

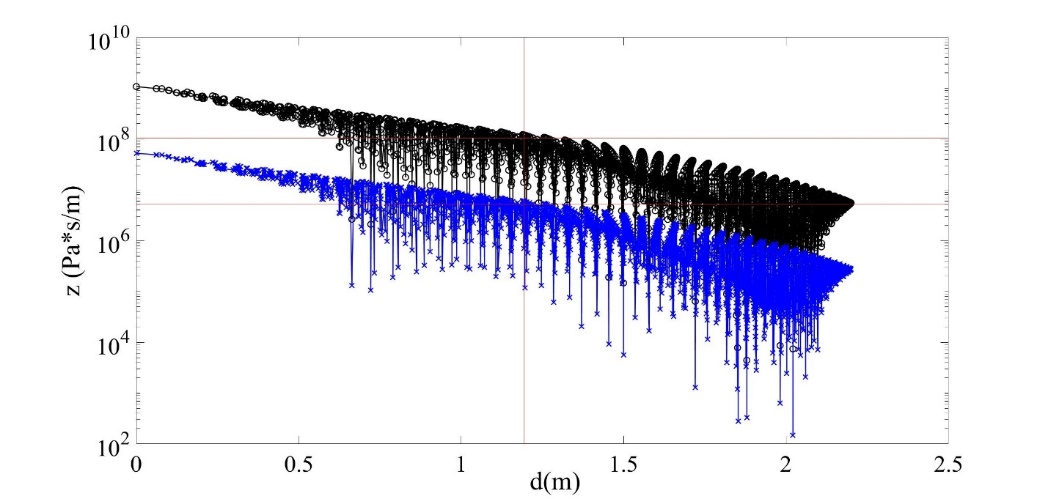
Figure 2. Magnitudes of the global acoustic impedance of the elastic spherical shell against the distance between surface elements. Black solid line: at 100 Hz. Blue solid line: at 2000 Hz. (Image by IACAS)

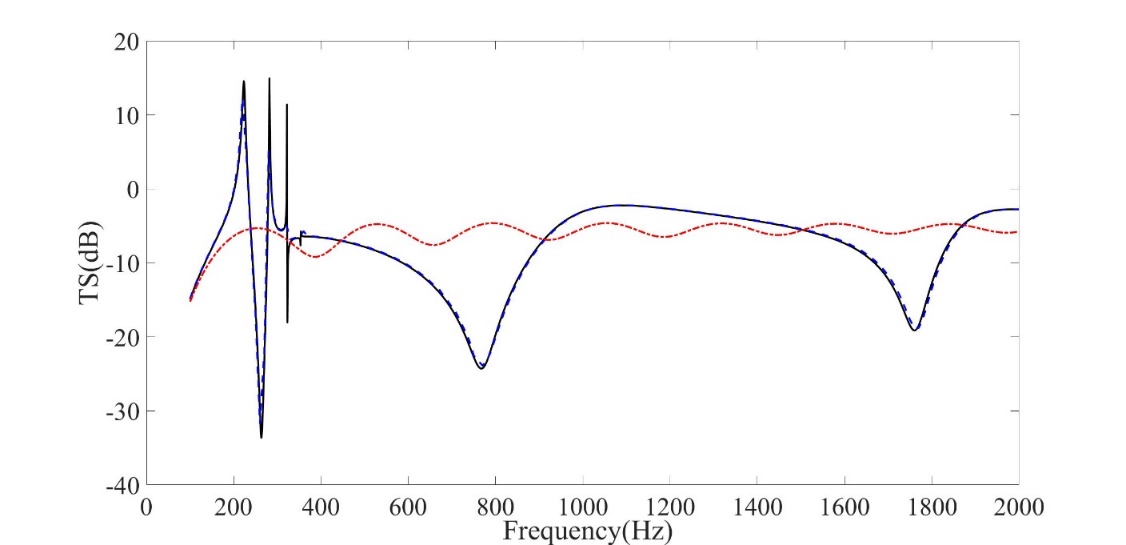
Figure 3. TS of the elastic spherical shell in-water under the incidence of plane wave. Solid line (black): series solutions. Dashed line (blue): numerical results. Dash-dotted line (red): hard-wall results. (Image by IACAS)

The research, published online in Journal of Theoretical and Computational Acoustics, was supported by the National Natural Science Foundation of China and the IACAS Young Elite Researcher Project.

Reference:

JIN Zhongkun, GAO Yan, WU Xianjun, YANG Jun. Global acoustic impedance for the analysis of acoustic scattering from elastic structures, Journal of Theoretical and Computational Acoustics. DOI: 10.1142/S2591728520500310