The Kalman filter, as one of the most celebrated adaptive algorithms, has been widely used in various applications. However, the Kalman filter was not fully investigated in the application of acoustic system identification for a long time. In 2006, the frequency-domain Kalman filter was successfully developed for echo cancellation based on a spectral process and observation noise covariance model. A subband Kalman filter was proposed in 2015, but its convergence is degraded due to the aliasing effects.
Recently, researchers at the Institute of Acoustics (IOA) of the Chinese Academy of Sciences proposed a new subband Kalman filter for the system identification problem to avoid the aliasing effect with improved convergence performance.
The paper entitled “Multiband-Structured Kalman Filter” was published online in IET Signal Processing.
The desired signal and the input signal are partitioned into N subband signals by means of analysis filters. By considering the past P input vectors in each subband, researchers construct the so called observation equation. The state equation is used to describe the evolution of the system response as time. The accurate model of the true system response is rather complex. To make the problem tractable, researchers use a first-order Markov model to describe the time-varying system. The new subband Kalman filter is thus derived under the umbrella of Kalman filter theory.
However, direct implementation of the proposed subband Kalman filter is expensive. Researchers hence present several approaches to reduce the computational complexity. Researchers employ the fast exact filtering approach to reduce the complexity of the filtering and update, which is originally proposed in their previous work (YANG Feiran, et al. Low-complexity implementation of the improved multiband-structured subband adaptive filter algorithm, IEEE Trans. Signal Process. 2015). Then, a new method is proposed to solve the matrix inversion efficiently, which can use a time-varying regularization parameter. The complexity of the fast SMSKF algorithm is approximately O(3M)-O(4M) multiplications per sample ( M being the filter length), which is attractive in practice.
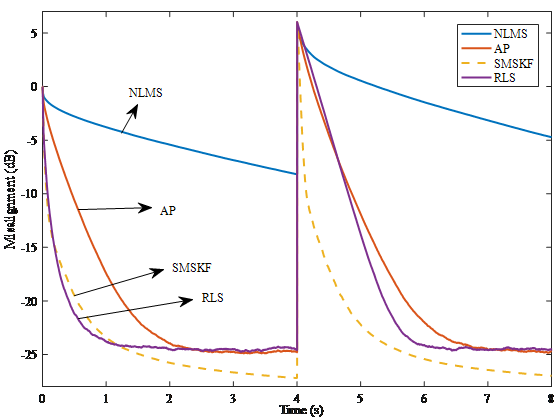
Figure 1. Misalignment of the NLMS, AP, SMSKF, and RLS algorithms. The input signal is an AR(10) process. (Image by YANG Feiran)
Extensive simulations are carried out to verify the performance of the new method. As figure 1 shows, the proposed method achieves a better trade-off between the convergence performance and computational complexity than RLS.
This research was supported by the National Natural Science Foundation of China (No. 61501449) and China Scholarship Council (No. 201504910058).
Reference:
YANG Feiran, YANG Jun. Multiband-Structured Kalman Filter. IET Signal Processing (Volume 12, August 2018, Pages 722-728). DOI: 10.1049/iet-spr.2017.0313.
Contact:
WANG Rongquan
Institute of Acoustics, Chinese Academy of Sciences, 100190 Beijing, China
E-mail: media@mail.ioa.ac.cn


