In the seismic (caused by or relating to an earthquake) modeling, due to small storage and fast computation speed, the second order finite difference scheme is a powerful tool, especially in irregular regions by using curvilinear grids. Unfortunately, numerical dispersion affects the performance of second order finite difference method. As a result, high order spatially accurate finite difference methods are required.

However, in irregular regions, high order methods are restricted because of the stability problem. The summation-by-parts finite difference operator, which is a natural way for wavefield simulation and leads to an attractive stability property, offers a way to obtain a stable and high order finite difference method in irregular regions.

In irregular regions, to realize the acoustic wavefield simulation and reverse time migration, researchers recently extends the second order summation-by-parts finite difference method to the fourth order case. The fourth order accuracy finite difference scheme is known advantageous in reducing memory and improving efficiency.

The summation-by-parts finite difference scheme is adopted on non-staggered grids to discretize the reformulated acoustic wave equation and perfect matched layers. The discretization is fourth and second order accuracy in space and time respectively. The application of summation-by-parts operator in boundary-conforming grids leads to an attractive stability advantage over traditional central finite difference scheme.

The elliptic method is applied for boundary-conforming grid generation, through the transformation by elliptic partial differential equations. After the boundary- conforming grids are generated, the two-dimensional acoustic wave equation is reformulated from Cartesian coordinate system into the curvilinear one. The second order displacement formulation is compactly reformulated for wavefield simulation and reverse time migration in irregular regions.

Simultaneously, the symmetric and compact form of time domain perfectly matched layers expressed in curvilinear coordinate system are applied to suppress artificial reflections. And then, the fourth order summation-by-parts finite difference operators are used to discretize these equations.

Based on the discretization, the acoustic wavefield simulation and reverse time migration can be realized through iterations. Meanwhile, the stability analysis of the scheme is given.

Finally, numerical experiments are presented to compare the accuracy of the second with fourth order summation-by-parts finite difference methods and to evaluate the efficiency of reverse time migration by using these two methods.

As well, comparisons are performed between the fourth order accuracy summation-by-parts finite difference method and central finite difference method to illustrate the stability superiority of summation-by-parts operators.

Fig. 1 and 2 are some results of wavefield simulation and reverse time migration by fourth order summation-by-parts finite difference method. Additionally, the methods of second and fourth order summation-by-parts finite difference method are compared in the aspects of time and storage requirement of reverse time migration per shot, as illustrated in Table 1.

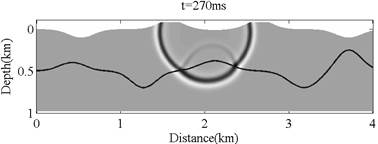
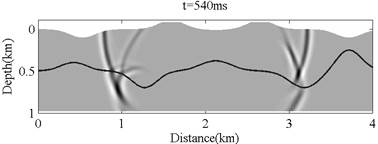
Fig. 1 Results of acoustic wavefield simulation (Image by WANG Ying et al.)

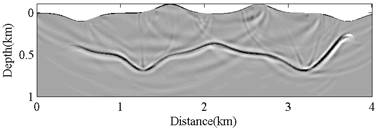
Fig. 2 Result of reverse time migration (Image by WANG Ying et al.)

Table 1 Time & storage requirement of reverse time migration per shot by second & fourth order summation-by-parts finite difference method (Table by WANG Ying et al.)

With the generation of boundary-conforming grids, the surface topography and irregular interfaces can be described precisely, which guarantees accurate modeling and avoids the stair-case approximation in irregular regions.

Particularly, the summation-by-parts operator ensures the stability of discretization in boundary-conforming grids. Compared with the second order summation-by-parts finite difference method, the application of the fourth order one in space can suppress the numerical dispersion, and significantly improve the efficiency and decrease the storage in reverse time migration.

Reference：

WANG Ying, ZHOU Hui, YUAN Sanyi, and YE Yameng. A Fourth Order Accuracy Summation-by-parts Finite Difference Scheme for Acoustic Reverse Time Migration in Boundary-Conforming Grids. Journal of Applied Geophysics (Volume 136, January 2017, pp. 498–512). DOI: 10.1016/j.jappgeo.2016.12.002

Contact:

WANG Ying

Institute of Acoustics, Chinese Academy of Sciences, 100190 Beijing, China

Email: wangying@mail.ioa.ac.cn