Since first reported back in 1986, the surface acoustic wave resonator configuration for mass sensor applications has long been researched. Design of the resonator plays a significant role in the improvement of the mass sensitivity, especially the sensitive areas. However, there is a gap in the research of the mass sensitivity associated with the sensitive areas of the surface acoustic wave devices.
To solve this problem, researchers from the Institute of Acoustics (IOA) of the Chinese Academy of Sciences propose a two-port Rayleigh surface acoustic wave resonator structure with three IDTs to analyze the mass sensitivity. They provide theory and experimental analysis of the mass sensitivity variation for different sensitive areas of a Rayleigh surface acoustic wave resonator.
The theoretical results are obtained to determine the optimal sensitivity area and verified by the measured responses. The optimal sensitivity area of a two-port Rayleigh surface acoustic wave resonator with three IDTs is the center IDT. And the sensitivity variation is strong across the surface. Results in this research can guide the detection position choice for surface acoustic wave sensors.
In the theoretical analysis, a 3-dimensional finite element method approach is established to extract the coupling-of-modes parameters in the absence and presence of mass loading covering the electrode structures.
In finite element method analysis, the modal analysis is adopted to extract the vibration modes at two eigenfrequencies (fsc− and fsc+ ). In the following, the harmonic frequency response is used to extract the harmonic admittance Y(β, ω). At last, the stationary analysis is utilized to extract the static capacitance.
After all the coupling-of-modes parameters are extracted by finite element method above, the coupling-of-modes model is used to simulate the frequency response of a Rayleigh surface acoustic wave resonator by a P-matrix cascading technique. Cascading the P-matrixes of unloaded areas with mass loaded areas, the sensitivity for different sensitive areas is obtained by analyzing the frequency shift, shown in Fig. 1. Finally, the performance of the sensitivity analysis is confirmed by the measured responses from the silicon dioxide (SiO2) deposited on different sensitive areas of Rayleigh surface acoustic wave resonators (Fig. 2).
This research has shown that the optimal sensitive area is focused on the center IDT, which just occupies 8% of the whole surface. And the sensitivity variation is strong across the surface. Based on the mass sensitive area analysis, the detection position choice for surface acoustic wave sensors can be guided.
It plays a significant role in the improvement of the mass sensitivity. A lower detection limit will be provided when optimal design is performed in surface acoustic wave gas chromatogram sensors, and larger sensitivity and cost reductions for surface acoustic wave chemical sensors.
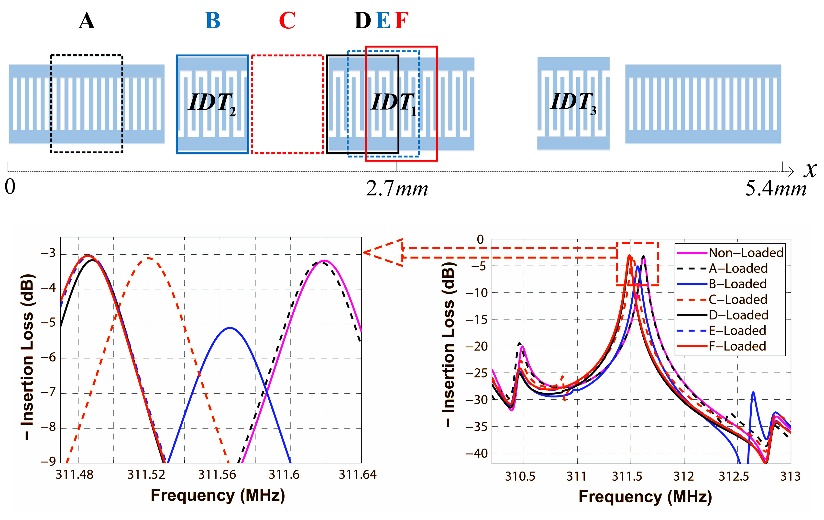
Fig. 1 The frequency responses for non-loaded and different sensitive areas along the x-axis from A to F with mass loaded of the two-port surface acoustic wave resonator (Image by IOA).
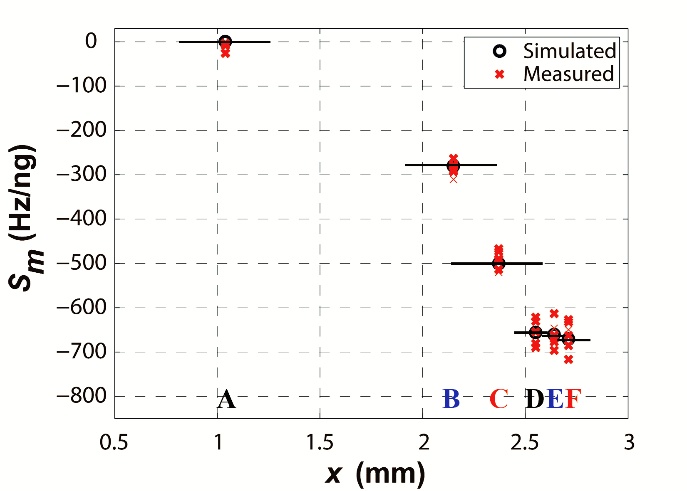
Fig. 2 The simulated and measured mass sensitivity for different surface areas, each position being demonstrated by repeated measurements (Image by IOA).
Reference:
HAO Wenchang, LIU Jiuling, LIU Minghua, LIANG Yong and HE Shitang. Mass Sensitivity Optimization of a Surface Acoustic Wave Sensor Incorporating a Resonator Configuration. Sensors 2016,
Contact:
HAO Wenchang
Institute of Acoustics, Chinese Academy of Sciences, 100190 Beijing, China


