In a shallow water waveguide, the low-frequency acoustic field can be viewed as a sum of dispersive normal modes. Based on the dispersive characteristics of an ideal waveguide with perfect reflection boundaries, the warping operator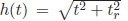 
is used to filter normal modes from the impulsive signal. Or, it can filter modes’ cross-correlation component from signal autocorrelation function through time-axis stretching or compression, where tr is the arrival time of the signal.
However, it should be noted that this warping operator is valid for a signal consisting of reflection dominated modes. In other words, it is suitable for the shallow water waveguides with a waveguide invariant approximately equal to one.
A waveguide-invariant-based warping operator (β-warping operator) suitable for both reflected and refracted modes in shallow water at low frequency is presented by QI Yubo, ZHOU Shihong, ZHANG Renhe and REN Yun from the Institute of Acoustics of the Chinese Academy of Sciences.
They have provided an effective tool to filter the cross-correlation function of modes from the signal autocorrelation function by a single hydrophone.
To obtain the warping operator, a formula is derived for the instantaneous phase of the cross-correlation function of two modes through an inverse Fourier transform of the phase expression in the frequency domain. And it is based on the horizontal wavenumber difference described by the waveguide invariant. The corresponding waveguide-invariant-based warping operator and its connection with the traditional operator are presented.
When the waveguide invariant approximately equals unity, both the β-warping operator and the traditional operator can transform the cross-correlation function to a monotone frequency. Otherwise, only the β-warping operator is suitable.
Once the signal autocorrelation function is transformed into warped monotones, the conventional modal filtering techniques can be used to filter the separated mode pairs.
The measured phases at different frequencies of the filtered modes’ cross-correlation function in the frequency domain contain source range information. So using the phase information and wavenumber difference calculated by a normal mode model, single hydrophone passive source ranging is realized (e.g. Fig.1 illustrates the source ranging result of an experimental signal using the filtered cross-correlation function of modes 1 and 2 while the real source range is 25.2 km).
This research was supported in part by the National Natural Science Foundation of China under Grant Nos. 11174312 and 11125420.
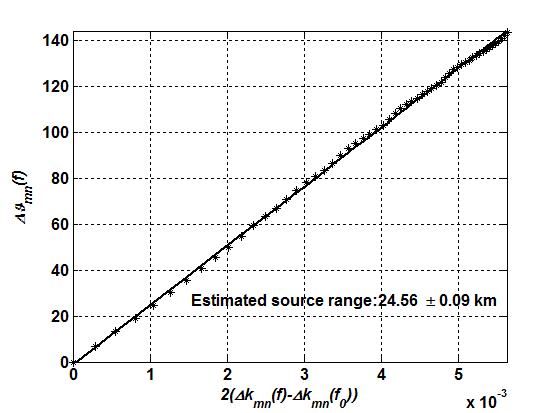
Fig. 1. Source ranging result of an experimental signal by linear regression between the measured phases of the filtered cross-correlation function of modes 1 and 2 and wavenumber differences for the silt sand sediment computed by KRAKEN (Image by QI).
References:
QI Yubo, ZHOU Shihong, ZHANG Renhe and REN Yun. A Waveguide-Invariant-Based Warping Operator and Its Application to Passive Source Range Estimation. Journal of Computational Acoustics (Vol. 23, NO. 1 (2015) 1550003, March 2015). DOI: 10.1142/S0218396X15500034
Contact:
QI Yubo
State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences, 100190 Beijing, China
Email: qyb@mail.ioa.ac.cn