In underwater acoustics, signals propagating in shallow water waveguide can be decomposed into a set of modal components, which exhibit dispersive characteristics. Recently, warping operators, which are designed to compensate for the dispersive effect and isolate the modal components, have been introduced as signal-processing tools to improve the modal separability. However, the warping operators used in most journal literature were built based on the ideal waveguide or the Pekeris model.
The theoretical analysis of warping operators for non-ideal shallow water waveguides is presented by NIU Haiqiang, ZHANG Renhe (CAS member) and LI Zhenglin from the Institute of Acoustics, Chinese Academy of Sciences. Different from the warping transformation defined using an ideal waveguide model, an improved warping operator is proposed based on the beam-displacementray-mode theory which can be adapted to low-frequency signals in a general shallow water waveguide.
For the sake of obtaining the warping operators for the general waveguides, the dispersion formula is first derived. The approximate dispersion relation can be achieved with adequate degree of accuracy for the waveguides with depth-dependent sound speed profiles and acoustic bottoms. In the following, the warping operators can be derived by integrating thedispersion formula. The derived dispersion relation and the corresponding warping operators are validated by numerical simulations. The performance of the proposed warping operator is verified for different waveguide models (e.g. Fig.1 for the general waveguide with a depth-varyingprofile in sea water). Besides, the comparison of different warping operators is given when there is an environmental mismatch in the warping model (see Fig.2). Once the original signal is transformed into warped modes, the conventional modal filtering techniques can be used to extract the separate modes.
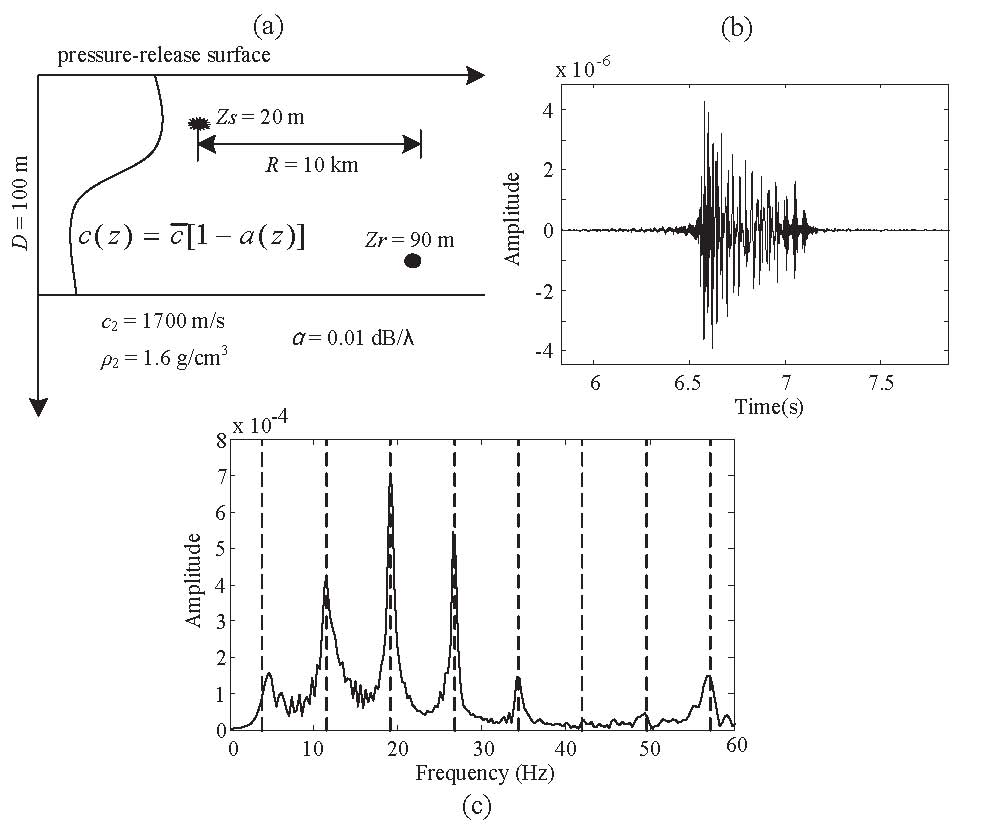
Fig.1 Warping transformation for the general waveguide with a depth-varying profile in sea water. (a) Environmental parameters of the waveguide. (b) Simulated signal in time domain with frequency band 20–200 Hz. (c) Frequency spectrum of the warped signal (Image by NIU).
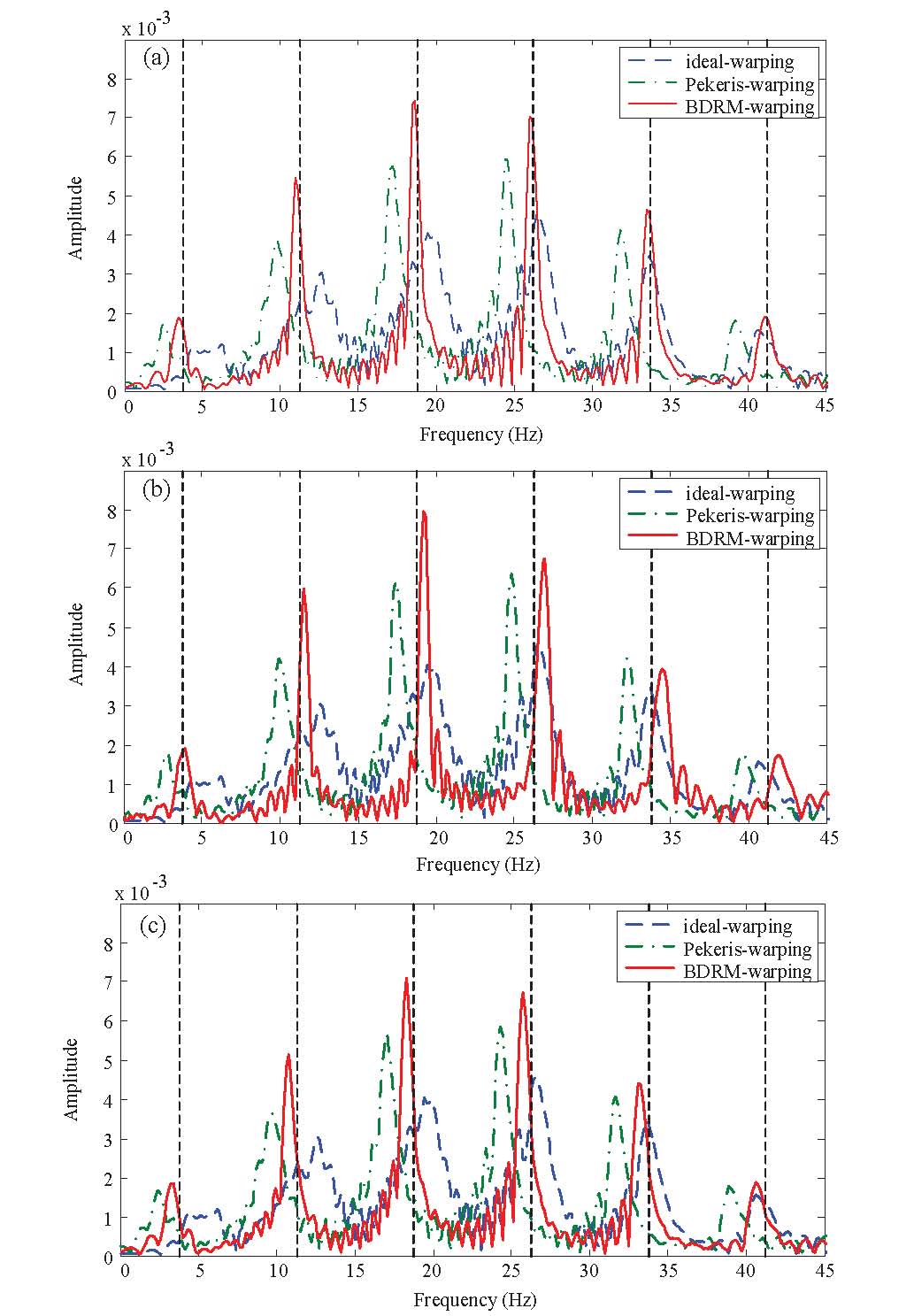
Fig.2 Comparison of the frequency spectra for different warping transformations. (a) Warping transformations without model mismatch (i.e., the bottom sound speed in warping model is 1650 m/s). (b) Warping transformations with model mismatch. The bottom sound speed in warping model is 1600 m/s. (c) Warping transformations with model mismatch. The bottom sound speed in warping model is 1700 m/s. In (a), (b), and (c), the dashed straight lines denote the theoretical frequencies (Image by NIU).
This research was supported by the National Natural Science Foundation of China (Grant Nos. 11174312 and 11074269).
References:
NIU Haiqiang, ZHANG Renhe, LI Zhenglin. Theoretical Analysis of Warping Operators for Non-ideal Shallow Water Waveguides. Journal of the Acoustical Society of America (vol. 136, no. 1, pp. 53-65, July 2014).DOI: 10.1121/1.4883370
Contact:
NIU Haiqiang
State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China
Email: nhq@mail.ioa.ac.cn


