Underwater acoustics is often used for environmental estimation and source localization. And the normal mode theory is an effective method for describing and analyzing the acoustic field. Recently, warping operators have been introduced as signal-processing tools to improve the modal separability. Once the normal modes are isolated and filtered, the dispersion curves are easily achieved. Many researchers have used the warping operator adapted in waveguides.
A modified warping operator for homogeneous shallow water based on the Beam-Displacement Ray-Mode (BDRM) theory is presented by NIU Haiqiang, ZHANG Renhe (CAS member) and LI Zhenglin from the Institute of Acoustics, Chinese Academy of Sciences. According to the BDRM theory, the contribution of the beam displacement and the time delay to the group velocity can be easily considered in a shallow water waveguide. A more accurate dispersion formula is derived by using the cycle distance formula to calculate the group velocity of normal modes. The derived dispersion formula can be applied to the homogeneous shallow water waveguide.
Theoretically, the formula is related to the phase of the reflection coefficient and suitable for various bottom models. Furthermore, based on the derived dispersion relation, the modified warping operator is developed to obtain linear modal structures. For the Pekeris model, the formulae for the phase of the reflection coefficient are derived in this research. By taking account of the effect of the bottom attenuation on the reflection coefficient, the formula for the phase of the reflection coefficient including the bottom attenuation is obtained for the Pekeris model with a lossy bottom.
Performance and accuracy of different formulae are evaluated and compared. Numerical simulations are done to investigate the performance of the dispersion formula and the modified warping operator for the Pekeris model. By comparison with the theoretical calculations, the modified dispersion formulae have better precision than the formula (see Fig.1). In addition, from the numerical results, it is found that neglecting the attenuation of bottom can lead to large errors around the cutoff frequencies for the arrival time of normal modes. As one might expect, the performance of the Pekeris unitary operator has been improved by modifying the dispersion formula.
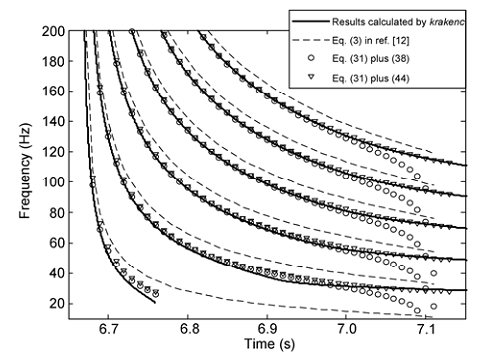
Fig.1 Comparison of the dispersion relation calculated by different formulae (Image by NIU).
The unitary operators or warping transformations as signal-processing tools have received considerable attention in the ocean acoustic community. Modal filtering techniques can be developed using these transformations. In this research getting under way, the researchers expect to achieve a dispersion formula with an adequate accuracy for the environmental model with an arbitrary sound speed profile in sea water.
This research was supported by the National Natural Science Foundation of China (Grant Nos. 11174312 and 11074269).
Journal References:
NIU Haiqiang, ZHANG Renhe and LI Zhenglin. A Modified Warping Operator Based on BDRM Theory in Homogeneous Shallow Water. SCIENCE CHINA-PHYSICS MECHANICS & ASTRONOMY (vol. 57, no. 3, pp. 424-432, MAR 2014). DOI: 10.1007/s11433-013-5243-x
Corresponding author:
NIU Haiqiang, State Key Laboratory of Acoustics,Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China
Email: nhq@mail.ioa.ac.cn


