For ensuring the reliability and security of bonding structures in service, it is of substantial significance to develop an effective model to characterize the interface between two solids.
Usually, the complexity of the interface makes it almost impossible to describe its mechanical behaviors explicitly. Furthermore, considering the difficulty of the inverse problem of the interfacial parameter identification, the model that can describe the interfacial properties with as few parameters as possible is strongly required.
The interaction of ultrasonic waves with the interface between two solids has been the subject of numerous investigations. At an early stage of the degradation of materials, the linear acoustic parameters such as sound velocity and attenuation often show little variation, but the nonlinear acoustic parameters may change significantly.
AN Zhiwu, WANG Xiaomin, MAO Jie, LI Mingxuan from the State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences (IACAS) establish a generalized nonlinear spring model through which the nonlinear reflection and transmission of an oblique incident longitudinal or shear wave at an interface can be effectively described under the limit of small layer thickness to wavelength ratio.
Numerical calculations have demonstrated the applicability of the nonlinear spring model that describes the interfacial properties with fewer parameters (Fig. 1). The accuracy of the nonlinear spring model developed depends on adhesive thickness, mass density and incident angle etc. To evaluate the model's applicability for certain interfacial structures, all the factors mentioned above should be taken into account. Generally speaking, smaller thickness, incident angle and lower mass density will make the model more accurate. It is of fundamental significance in the nondestructive evaluation of bonding interface by nonlinear ultrasonics.
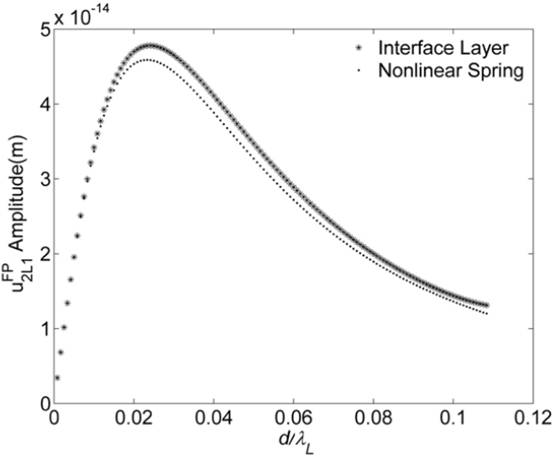
(a) Longitudinal second harmonic (Image by IACAS)
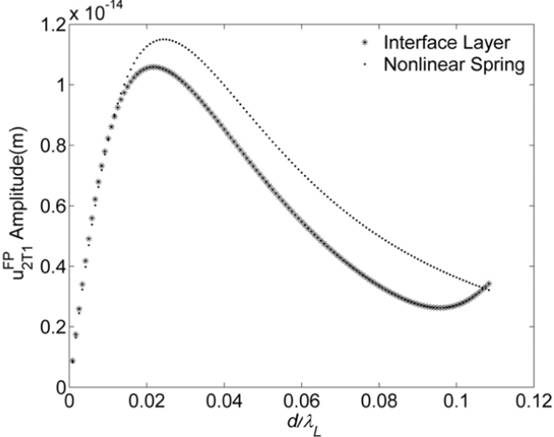
(b) Transverse second harmonic (Image by IACAS)
Fig. 1. Comparison of nonlinear spring model with interface layer model for displacement amplitudes of transmitted second harmonic from an aluminum–epoxy–aluminum structure at an incident angle of 0.6 rad.
The relevant research article entitled “A Nonlinear Spring Model for an Interface between Two Solids” was released online: http://dx.doi.org/10.1016/j.wavemoti.2012.09.004 and on the journal of Wave Motion (Volume 50, Issue 2, March 2013, Pages 295–309).
CONTACT:
AN Zhiwu
Institute of Acoustics, Chinese Academy of Sciences
E-mail: anzhiwu@mail.ioa.ac.cn


