Sound propagation in a wedge-shaped waveguide with perfectly reflecting boundaries is one of the few range-dependent problems with an analytical solution. Hence, it provides an ideal benchmark for a full two-way solution to the wave equation.
An analytical solution for the sound propagation in an ideal wedge with a pressure-release bottom was presented in the year of 1990. The ideal wedge problem with a rigid bottom is also of great importance in underwater acoustics.
Currently, an exact analytical solution to the ideal wedge problem with a perfectly reflecting bottom, either rigid or pressure-release is proposed by LUO Wenyu, YANG Chunmei, QIN Jixing, ZHANG Renhe who is one of the Chinese Academy of Sciences(CAS) Members from the State Key Laboratory of Acoustics, Institute of Acoustics, CAS (IACAS). This proposed analytical solution can be used as a primary range-dependent benchmark to establish the accuracy of numerical models.
In addition, the recently developed numerical step-wise coupled-mode model, DGMCM is applied for addressing the problem of sound propagation in an ideal wedge. Closed-form expressions for the coupling matrices for propagation in waveguides bounded above by a pressure-release sea surface and below by a rigid or pressure-release bottom are also given.
Comparisons of the results by the analytical solution and the numerical model DGMCM are shown in Fig.1 for the pressure-release-bottom case and Fig.2 for the rigid-bottom case, both of which show excellent agreement between these two methods, indicating that the proposed analytical solution and DGMCM are still valid for large slope angles.
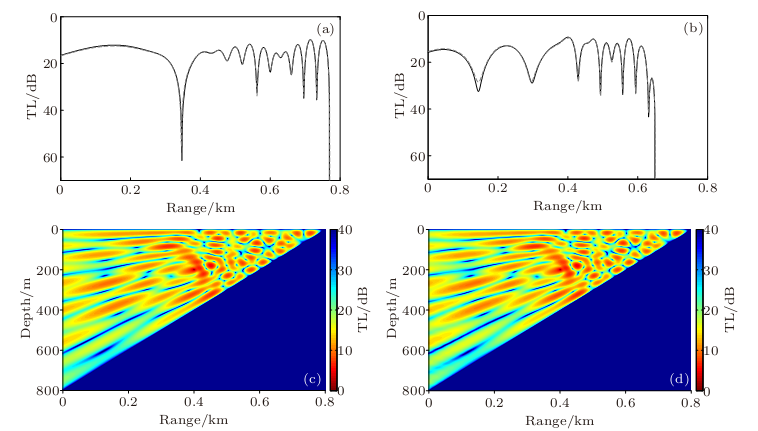
Fig.1. Comparison between the analytical solution and DGMCM for the pressure-release-bottom case with the slope angle of 45. (a) TL at 30-m depth; (b) TL at 150-m depth; (c) TL versus range and depth in the analytical solution; (d) TL versus range and depth in DGMCM. In panels (a) and (b), the black solid line is the analytical solution and the gray dashed line is the DGMCM result (Image by IACAS).
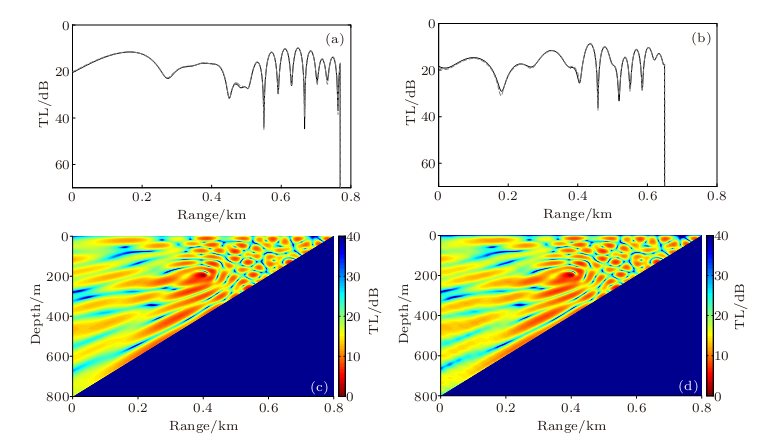
Fig. 2. Comparison between the analytical solution and DGMCM for the rigid-bottom case with the slope angle of 45. (a) TL at 30-mdepth; (b) TL at 150-m depth; (c) TL versus range and depth in the analytical solution; (d) TL versus range and depth in DGMCM. In panels (a) and (b), the black solid line is the analytical solution and the gray dashed line is the DGMCM result (Image by IACAS).
Theoretically, as also confirmed by numerical simulations, the proposed analytical solution for sound propagation in ideal wedges is valid for any frequency and any slope angle. Note that with the use of the proposed closed-form expressions for the coupling matrices, the numerical model DGMCM can be applied to general range-dependent waveguides characterized by a homogeneous water column, a pressure-release surface, and a rigid or pressure-release bottom, not necessarily wedge-shaped waveguides. Moreover, this model can be easily generalized to more realistic waveguides. For this purpose, a numerical normal mode model such as KRAKEN should be adopted to provide local modal solutions and their associated coupling matrices.
The research entitled “Benchmark Solutions for Sound Propagation in an Ideal Wedge” has been published online: http://iopscience.iop.org/1674-1056/22/5/054301 and on the journal of Chinese Physics B (Vol. 22, No. 5, 2013,054301, DOI:10.1088/1674-1056/22/5/054301).
Contact:
LUO Wenyu
Institute of Acoustics, CAS
E-mail: lwy@mail.ioa.ac.cn


