Direction-of-arrival (DOA) estimation has been paid a lot of attention to by variety of research areas. Many high-resolution DOA estimation algorithms have been proposed, including MUSIC and ESPRIT. However, most of these methods are subspace-based and will not work when the snapshot number is limited.

So LI Xuan, MA Xiaochuan, YAN Shefeng, and HOU Chaohuan (CAS Member) proposed a high-resolution method with single snapshot on the basis of the compressive sampling theory.

Compressive sampling (CS), or compressed sensing has made a lot of progress in the last decade and its impressive performance has been reported in several applications such as fusion of images, ultra wideband communications and underwater acoustic communications.

CS is introduced to single snapshot DOA estimation. To establish the high-resolution method, at first, a novel signal model is proposed by sampling sparsely in the spatial domain. The high-resolution DOA estimation can be described with an underdetermined equation solving problem. And then, the CS techniques are employed to solve the underdetermined system, such as Diagonal Loading Least Squares (DLLS), ℓ1 Regularization, and Orthogonal Matching Pursuit (OMP). In numerical simulations, all of these three CS methods can estimate DOA accurately in Fig. 1.

Fig. 1 DOA estimation in the single snapshot scenario when sensor number = 30, and source number = 5 (Image by IACAS).

Shown in Fig. 2, it is clear that the CS methods are robust for both coherent and incoherent signals, and can be applied in scenario of single snapshot, while MUSIC requires snapshot number larger than sensor number. Moreover, the CS methods are still effective when sources number is greater than sensor number in Fig. 3.

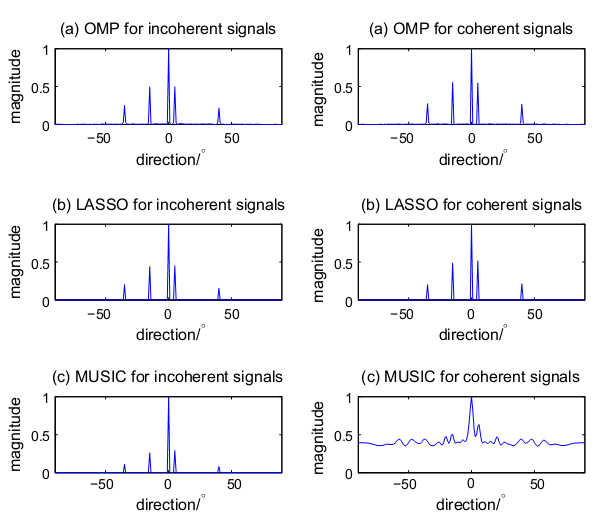
 Fig. 2 Uncorrelated and correlated signals DOA estimation by MUSIC and CS (Image by IACAS).

 

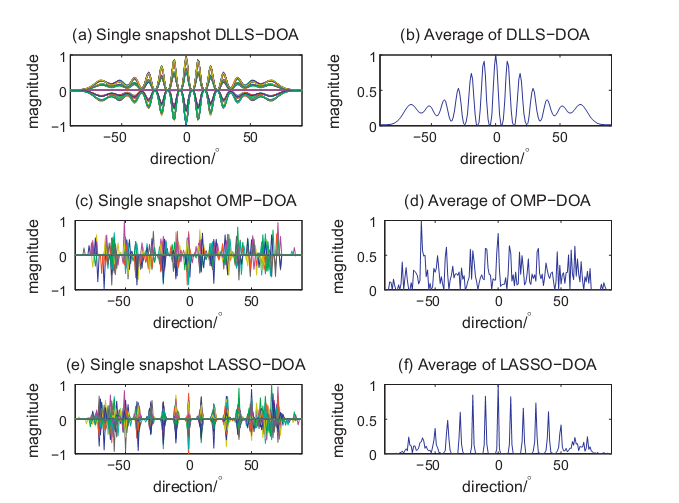
Fig. 3 DOA estimation when M = 14, K = 15(Image by IACAS).

Simulations reveal the proposed method’s excellent performance. In comparison with MUSIC, the high-resolution method has several advantages. It can be applied in the single snapshot scenario. Besides, it escapes from estimating source number and it does not need to restrict the sources' correlativity. Furthermore, it can keep working when the sensor number is less than source number, and it works well when the sources are coherent.

The research production will be published on Applied Acoustics (Vol. 74, No. 7, Pages 926-930, 2013).