In last few years, there has been a growing interest in adaptive filtering applications, such as channel equalization, adaptive noise cancellation, and acoustic echo cancellation. Among them, the most common one is based on least mean-square (LMS) algorithm, because of its simplicity of the structure.

Since the simplicity of the adaptive filtering applications is important, to reduce the computational complexity, the frequency-domain block LMS (FBLMS) algorithm was developed.

Actually, there are two kinds of FBLMS algorithms: the constrained one and the unconstrained one. Only the constrained FBLMS algorithm is concerned in this research for better convergence performance. In Fig.1, this is the structure of the constrained FBLMS algorithm.

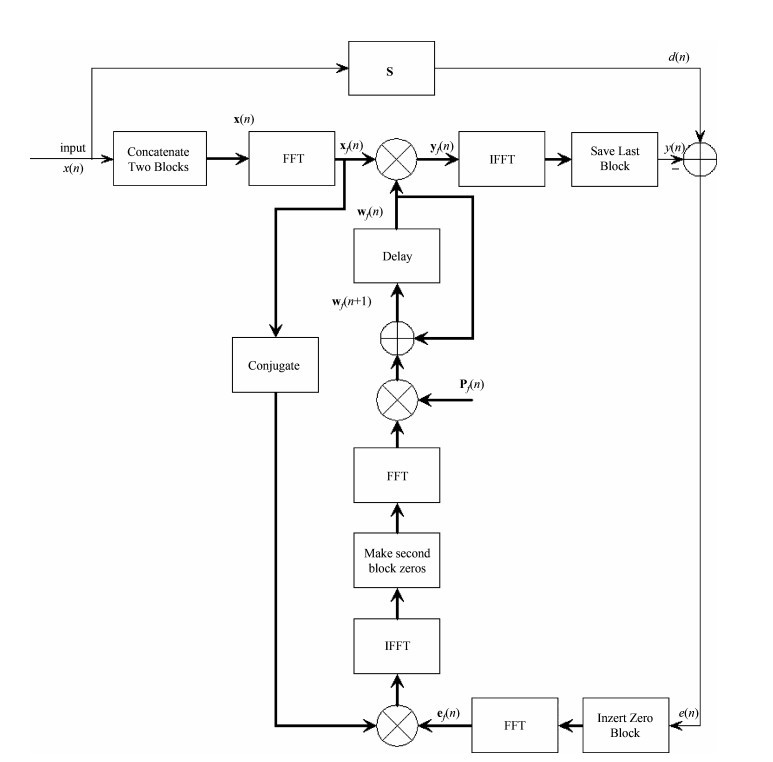
Fig.1  The constrained FBLMS algorithm

Until now, there has been much work in analyzing the performance of the FBLMS algorithm. In almost all analysis of the FBLMS algorithm, where the length of the system impulse response is extremely long, the adaptive filter usually works in an under-modeling situation.

As a result, the sufficient length FBLMS algorithm is not applicable to the deficient length case. In this correspondence, the steady-state solution of the deficient length constrained FBLMS algorithm is analyzed.

Simulations are proposed and show that, as for the deficient length FBLMS algorithm, the steady-state solution relies on the step size selected.

If the same step size is selected for each frequency bin, the FBLMS algorithm has the same convergence performance with BLMS algorithm and will converge to the Wiener solution (Wiener filter). However, if the normalized step size is selected for each frequency bin, the FBLMS algorithm will not be convergent to the Wiener solution and the steady-state solution of the adaptive filter depends on the autocorrelation of the input signal.

This research result was published online http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6298980  and on the recently issued IEEE Transactions on Signal Processing (Vol. 60, No. 12, Pages 6681-6687, Dec. 2012).